Imagem Matemática

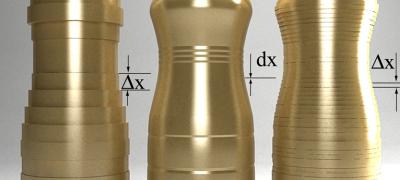
Olá pessoal, estou criando algumas imagens 3d com temas matemáticos, para ilustrar melhor conceitos que estou aprendendo no curso que estou fazendo.:) Aqui está uma das imagens, ilustrando o cálculo integral, a somatória e o uso para calcular volumes (no caso de um iogurte). Também mostrando para que serve o tal "dx" da integral (dx é espessura, não é enfeite; tem muita gente que faz integral e nem desconfia disso) Cada "rodela" é Pi*R^2 (círculo) * h (altura), ou seja, um cilindro. No caso, a altura é Delta X. O raio muda pra cada cilindro, e é denotado por f(x), para k. (k é o número da rodela). Quando as rodelas são finitas, contáveis, usamos a somatória (fórmula de baixo). Para calcular todas as rodelas possíveis, com espessura infinitamente pequena, usamos a integral acima, e delta x passa a ser chamado dx. Usei 3dsmax 8.0 SP3, e Vray 1.50 RC3

cara so pela matematica pra mim ta dez.heheheheheheh Eu adoro matematica, e quando parte pra raciocinio lógico, ai é q eu gosto!!!

Aceitar críticas constroi!!!

Nossa cara, vc confundiu a minha fraca mente! uhauhahuahua quanto ao render, ta bacana, ta precisando de mais samples, ou melhorar a qualidade do antialiasing pois estão desaparecendo as fissuras nas partes finas das peças. abraço

Quer dizer que essa formula toda é só pra calcular quantas rodelinhas dá pra colocar ai é.... puts Flw!!!

Afinal, considerando o raio da parte mais larga do pote igual a 4 centimetros quantos litros de iogurte caberia nesse troço?

Também fiquei confuso, não sou fã de matemática, mas seu trabalho em 3d ta bem interessante!

Sou aspirante a engenheiro.... Existe tal f(x) para esse objeto que voce criou?? A latinha do leito condensado da moca fo criada usando uma formula parecida, ela tem o menor material possivel para maior area interna e ainda um desgin chique.... Boa sorte nas suas experimentacoes.... preciso ir, tenho prova de calculo agora..... :-P

Antigo Ass_Killer de volta! Pagina pessoal RodrigoBill

hehehe, mto bom a metodologia p explicar a integral... valeu fabiocd. Comecei a cursar engenharia mas abandonei. Mas eh mais ou menos o seguinte: É facil calcular o volume de um cilindro (área da base x altura) Só que a embalagem de iogurte tem forma irregular(figura do meio). Então podemos pensar ela como sendo vários cilindrozinhos de alturas pequenas, ai calculamos cada um e somamos (figura da esquerda). Só que com isso vamos chegar a um valor aproximado, pois o perfil fica dentado, como uma escada, e na verdade a embalagenm eh suave. Ai que entra a integral, ela pega essa altura (delta x) e pensa ela como zero(figura da direita), algo muito próximo. Entao eh como se praticamente víssemos infinitos cilindrozinhos de altura tão pequena q podemos pensar q eh zero (o q seria circunferencias pois nao tem altura). Pensando assim, a formula chega no valor real do volume, pois tendemos o delta x a zero (dx) e teremos infinitos cilindrozinho de altura indo p zero. O perfil não fica dentado.

Heuew... agora esta explicado, porém vc não respondeu a minha pergunta ehim.. hahaha

Caio Lamas, auuahuaha Mas vc não deu os limites... heheh vai de quanto a quanto?(não precisa dizer, risos) Os raios variam de um valor minimo a um máximo. Pede ao fabiocd q ele te diz, hehehe. tou longe da engenharia. :-P